Funkcję określoną wzorem y = ax + b nazywamy funkcją liniową.
a – współczynnik kierunkowy prostej
b – wyraz wolny (współrzędna przecięcia wykresu funkcji z osią OY)
Wykresem funkcji liniowej jest prosta nachylona do osi OX pod kątem .
Dziedziną funkcji liniowej jest zbiór liczb rzeczywistych.
Aby sporządzić wykres funkcji liniowej należy:
– wyznaczyć przynajmniej dwa punkty, które należą do jej wykresu
– poprowadzić przez nie prostą.
Przykład 1
Sporządź wykres funkcji y = x + 1
1. Tworzymy tabelkę i w jej górnym wierszu wpisujemy dowolne iksy (należące do dziedziny funkcji).
2. Podstawiamy po kolei do wzoru funkcji argumenty {-1, 0, 1, 2} i obliczamy wartości funkcji, które wpisujemy w wierszu dolnym.
f(-1) = -1 +1 = 0, więc dla x = -1 mamy y = 0
f(0) = 0 + 1 = 1, więc dla x = 0 mamy y = 1
f(1) = 1 + 1 = 2, więc dla x = 1 mamy y = 2
f(2) = 2 + 1 = 3, więc dla x = 2 mamy y = 3
3. Zaznaczamy punkty w układzie współrzędnych.
4. Łączymy punkty i otrzymujemy wykres funkcji.
5. Podpisujemy prostą odpowiednim równaniem.
Spójrzcie na poniższy film, na którym dokładnie omawiam metody rysowania wykresów funkcji liniowych.
Jeżeli nie chcecie korzystać z metody zaprezentowanej na poprzedniej lekcji, to możecie wykorzystać inny sposób do rysowania wykresów funkcji liniowych.
Moim zdaniem jest on dużo przyjemniejszy od sporządzania tabelki.
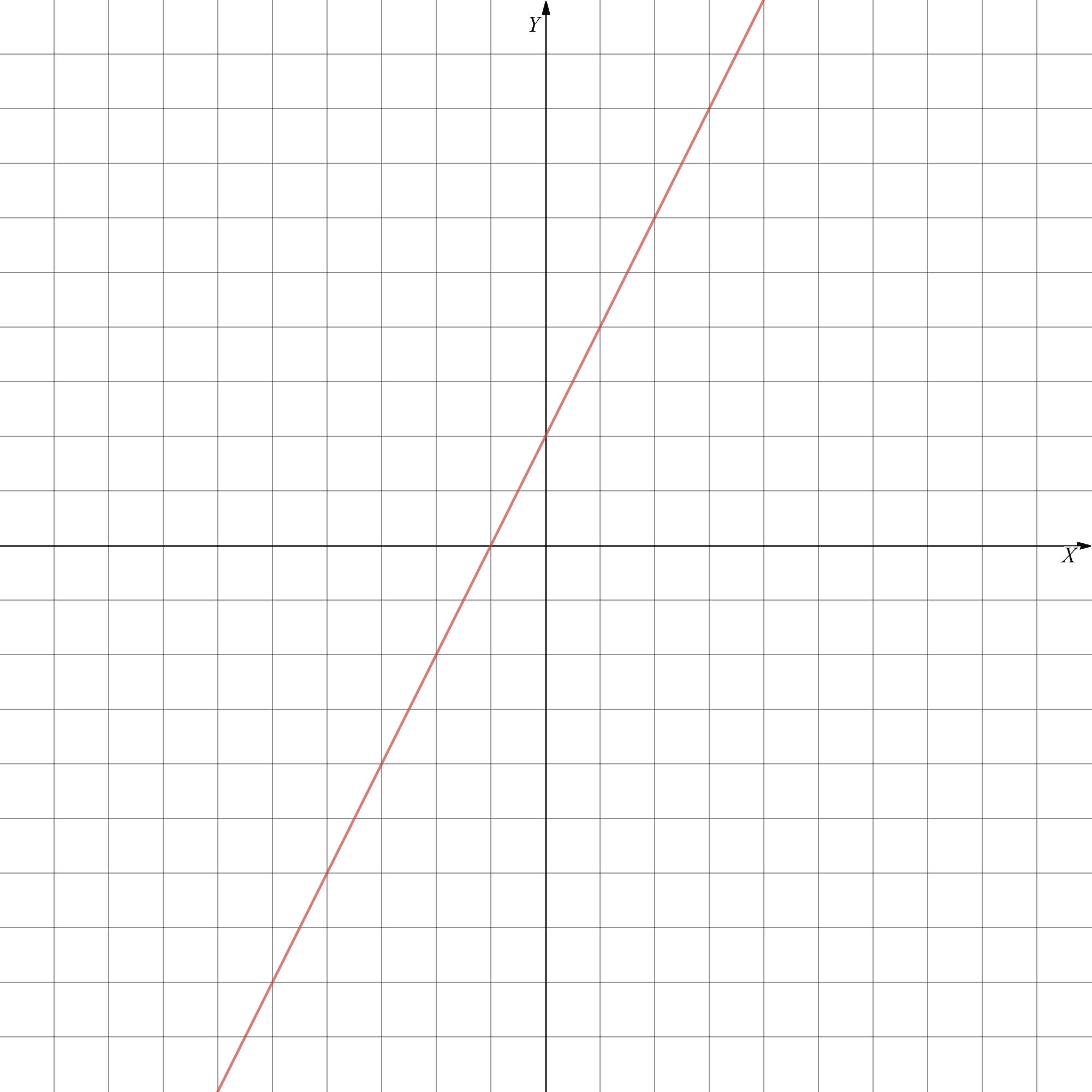
Punkt przecięcia wykresu każdej funkcji z prostą OY ma współrzędne (0,y), czyli pierwsza współrzędna takiego punktu jest zawsze równa 0, co możecie zobaczyć na poniższym rysunku.
Na rysunku punkt przecięcia wykresu funkcji z osią OY ma współrzędne (0,2).
Spójrzcie teraz na funkcję liniową y = ax + b.
W funkcji liniowej wykres funkcji przecina oś OY w punkcie o współrzędnych (0, b), gdzie b to wyraz wolny.
Przykład 1
Podaj współrzędne punktu przecięcia wykresu funkcji y = 2x – 4 z osią OY.
Rozwiązanie
Ze wzoru funkcji odczytujemy, że b = – 4.
Punkt przecięcia wykresu funkcji z osią OY ma współrzędne (0, b).
Zatem w naszym przypadku jest to punkt (0, – 4).
Miejsce zerowe to punkt przecięcia wykresu funkcji z osią OX.
Funkcja liniowa może posiadać:
- jedno miejsce zerowe
- nieskończenie wiele miejsc zerowych, gdy y = 0
- brak miejsc zerowych, gdy mamy do czynienia z funkcją stałą (oprócz y = 0).
Miejsce zerowe funkcji liniowej można wyznaczyć dwoma sposobami:
1. Podstawić w miejsce igreka 0 (y = 0) do wzoru funkcji.
Przykład 1
Wyznacz miejsce zerowe funkcji y = 2x + 4.
y = 2x + 4
0 = 2x + 4
– 2x = 4 |: (- 2)
x0 = – 2
Odp. Miejsce zerowe tej funkcji to x0 = – 2.
2. Skorzystać ze wzoru na miejsce zerowe :
Przykład 2
Wyznacz miejsce zerowe.
y = 2 x + 4 -> a = 2 oraz b = 4
Odp. Miejsce zerowe tej funkcji to x0 = – 2.
Przykład 3
Wyznacz miejsce zerowe funkcji o wzorze y = – 4x – 5.
I sposób
0 = – 4x – 5
4x = – 5 | : 4
II sposób
y = – 4 x – 5 -> a = – 4 oraz b = – 5
Funkcja liniowa może być rosnąca, malejąca lub stała.
Mając dany wzór funkcji liniowej jej monotoniczność odczytujemy po współczynniku kierunkowym prostej czyli a (liczbie stojącej przy iksie).
y = ax + b
a > 0 funkcja rosnąca
a < 0 funkcja malejąca
a = 0 funkcja stała
Przykład 1
Określ monotoniczność funkcji.
a) y= 2 x + 4
a = 2 , a > 0, funkcja rosnąca
b) y= -2 x + 5
a= – 2 , a < 0, funkcja malejąca
c) y = 3
a = 0, funkcja stała
d) y= 5 – 2 x
a= – 2 , a < 0, funkcja malejąca
e) y = 4 x + 2
a = 4 , a > 0, funkcja rosnąca
f) y = -1
a = 0, funkcja stała
Podsumujmy wiadomości zawarte w filmie.
Aby wyznaczyć równanie prostej przechodzącej przez dwa punkty A = (x1, y1) oraz B = (x2, y2) korzystamy z jednej z poniższych metod.
ze wzoru:
( y – y1)(x2 – x1) = (y2 – y1)(x – x1)
współrzędne obu punktów podstawiamy do wzoru y = ax + b i tworzymy układ równań, który następnie należy rozwiązać
wykorzystujemy wzór na współczynnik liniowy . Po jego obliczeniu podstawiamy wyznaczoną liczbę oraz współrzędne jednego z punktów do wzoru y = ax + b, a następnie wyznaczamy wyraz wolny (b).
Tym razem powiemy sobie kilka słów na temat dwóch postaci prostej :
– postaci kierunkowej
– postaci ogólnej
Postać kierunkowa ma następujący wzór :
y = ax + b
a – współczynnik kierunkowy prostej
b – wyraz wolny
Przykłady prostych w postaci kierunkowej
y = 2x – 4
y = – 3x – 2
y = 2
y = – 4
Postać ogólna ma następujący wzór :
Ax + By + C =0 ,
gdzie A i B nie mogą być jednocześnie równe 0.
Przykłady prostych w postaci ogólnej
2x – 4y + 5 = 0
-3x – y + 1 = 0
x + 3 = 0
y – 1 = 0
Zadanie 1
Naszkicuj prostą daną za pomocą równania 2x + y – 1 = 0.
Zadanie 2
Naszkicuj prostą daną za pomocą równania .
Jedna prosta może mieć wiele równań ogólnych. Szerzej mówię na ten temat w poniższym filmie.
Zadanie 3
Które z równań opisują tą samą prostą?
l : -2x + y + 1 = 0
k : -4x + 4y + 4 = 0
m : 20x – 4y – 12 = 0
n : – 15x + 3y + 9 = 0
o : – 4x + 2y + 1 = 0
p : – 10x + 2y + 6 = 0
Zadanie 4
Naszkicuj prostą o równaniu 2x – y +1 = 0. Podaj współrzędne punktów, w których przecina ona osie układów współrzędnych.
Zadanie 5
Zadanie 6
Zadanie 7
Wykresem funkcji liniowej y = ax + b jest prosta nachylona do osi OX pod kątem alfa, gdzie:
- Jeżeli kąt α jest ostry ( 0° < α < 90° ), to współczynnik kierunkowy jest dodatni
- Jeżeli kąt α jest rozwarty (90° < α < 180°) , to współczynnik kierunkowy jest ujemny
- Jeżeli α = 90°, wówczas nie podamy współczynnika kierunkowego, gdyż tg 90° nie istnieje.
- Jeżeli α = 0° lub α = 180°, to współczynnik kierunkowy wynosi 0 i mamy do czynienia z funkcją liniową stałą o równaniu y = b.
Więcej informacji na ten temat znajdziecie w poniższym filmie.
Zadanie 1
Podaj kąt nachylenia wykresu funkcji do osi OX.
Zadanie 2
Dla jakiego parametru m funkcja y = mx + 1 jest nachylona do osi OX pod kątem 30º ?
Zadanie 3
Podaj wzór prostej nachylonej do osi OX pod kątem 45º i przechodzącej przez punkt o współrzędnych (2, 3).
Zadanie 4
Wyznacz równanie prostej nachylonej do osi OX pod kątem 120º i przechodzącej przez punkt .
Zadanie 5
Znajdź równanie prostej nachylonej pod kątem 135º do osi OX i przechodzącej przez punkt A = (- 3, 5).
Mamy dwie proste:
y = a1x + b1
oraz
y = a2x + b2
Proste te będą równoległe, gdy ich współczynniki kierunkowe będą takie same.
a1 = a2
Proste równoległe oznaczamy symbolem „ ”.
Zapis oznacza, że prosta k jest równoległa do prostej m.
Proste równoległe są nachylone do osi OX pod tym samym kątem.
Zadanie 1
Zbadaj równoległość prostych :
a) y = – x oraz y = x – 1
b) y = 3x + 1 oraz y = 3x – 2
c) oraz
d) y = 3x – 5 oraz y = 6 + 3x
e) oraz
Zadanie 2
Podaj równanie prostej równoległej do przechodzącej przez punkt A = (2, 6).
Zadanie 3
Prosta o równaniu jest równoległa do y = 4x – 1, stąd wynika, że
Zadanie 4
Prosta l ma równanie . Wskaż równanie prostej równoległej do prostej l.
Zadanie 5
Prostymi równoległymi są proste o wzorach :
a) y = 4x – 1 oraz y = – 4x + 2
b) y = 2 – 4x oraz y = – 4x + 3
c) oraz y = x + 2
d) y = x oraz y = – x
Zadanie 6
Prosta równoległa do prostej o równaniu 2x – 4y +6 = 0 ma wzór :
a) y = – 2x – 3
b)
c) y = – 4x – 4
d)
Zadanie 7
Wskaż równanie prostej, która jest równoległa do prostej o równaniu 4x – 2y = 7.
a) y = 2x + 4
b) y = -2x – 4
c)
d)
Zadanie 8
Wskaż równanie prostej równoległej do prostej o równaniu 4x – 2y = 7.
a) y = 2x + 4
b) y = – 2x – 4
c)
d)
Zadanie 9
Współczynnik kierunkowy prostej równoległej do prostej o równaniu
y = – 4x + 6 jest równy :
a) 4
b) – 4
c)
d)
Zadanie 10
Wyznacz parametr m, dla którego prosta o równaniu y = (m – 1)x + 4
jest równoległa do prostej y = – 4x – 5.
Zadanie 11
Wiadomo, że proste o równaniach y = 3x + 4 oraz y = (2m + 2)x – 1
są równoległe. Wynika z tego, że :
a) m = – 2
b) m = 2
c) m =
d) m =
Zadanie 12
Wskaż prostą równoległą do prostej k danej równaniem
a)
b)
c)
d)
Zadanie 13
Wskaż równanie prostej równoległej do 5x + 3y + 4 = 0.
a)
b)
c)
d)
Zadanie 14
Podaj równanie prostej równoległej do y = 4x + 5 i przechodzącej przez początek układu współrzędnych.
Zadanie 15
Prosta k pokazana na rysunku jest równoległa do prostej l.
Wiedząc, że wykres prostej l przechodzi przez punkt A = (2, 4) podaj jej wzór w postaci ogólnej.
Mamy dwie proste:
y = a1x + b1
oraz
y = a2x + b2
Proste te będą prostopadłe, gdy:
a1 · a2 = – 1
Proste prostopadłe oznaczamy symbolem .
Zapis odczytujemy jako : prosta k jest prostopadła do prostej l.
Dwie proste są prostopadłe, gdy przecinają się pod kątem prostym.
Zadanie 1
Sprawdź czy proste oraz
są prostopadłe.
Zadanie 2
Sprawdź czy proste oraz l : y = – 5x + 1 są prostopadłe.
Zadanie 3
Oblicz współczynnik kierunkowy prostej k, jeśli jest ona prostopadła do prostej o wzorze .
Zadanie 4
Oblicz współczynnik kierunkowy prostej k, jeśli jest ona prostopadła do prostej o wzorze .
Zadanie 5
Wyznacz równanie prostej prostopadłej do y = – 3x + 2 i przechodzącej przez punkt (0, – 2).
Zadanie 6
Miejsce zerowe pewnej funkcji liniowej jest równe 4. Jej wykresem jest prosta prostopadła do prostej m : 2x + y – 4 = 0. Podaj równanie szukanej prostej w postaci kierunkowej.
Zadanie 7
Wyznacz równanie prostej prostopadłej do y = 2 i przechodzącej przez punkt A = (-3, 4).
Zadanie 8
Wyznacz równania prostych AB, AC, BC. Sprawdź czy trójkąt ABC jest prostokątny.
Zadanie 9
Podaj dla jakiego parametru m proste o równaniach y = 2mx – 1 oraz y = 4m²x+m² + 1 są prostopadłe.
Zadanie 10
Podaj parametr m, dla którego proste y = (m +2)x – 4 oraz x + 3 = 0 są prostopadłe.
Spójrzcie teraz na film, w którym podsumujemy informacje na temat współczynnika kierunkowego.
Rozwiązaniem układu równań jest punkt (punkty), w których proste będą się przecinały.
Układ równań liniowych może posiadać :
- jedno rozwiązanie
- brak rozwiązań
- nieskończenie wiele rozwiązań.
Wszystko dokładniej tłumaczę na poniższym filmie.
Zadanie 1
Rozwiąż układ równań metodą graficzną.
Zadanie 2
Rozwiąż układ równań metodą graficzną.
Współczynnik „a” określany jest dzięki monotoniczności funkcji.
Współczynnik „b” określany jest po miejscu, w którym wykres funkcji przecina oś OY.
Ćwiartki układu współrzędnych numerujemy przeciwnie do ruchu wskazówek zegara.
Zbierając razem wszystkie powyższe informacje przeanalizujmy kilka przykładów.
Przykład 1
Określ znaki współczynników a i b funkcji korzystając z wykresu.
a > 0, bo funkcja jest rosnąca.
b > 0 , bo wykres funkcji przecina oś OY powyżej osi OX, w punkcie (0,1).
Przykład 2
Określ znaki współczynników a i b funkcji korzystając z wykresu.
a > 0, bo funkcja jest rosnąca.
b < 0 , bo wykres funkcji przecina oś OY poniżej osi OX, w punkcie
(0, – 1).
Przykład 3
Określ znaki współczynników a i b funkcji korzystając z wykresu.
a = 0, bo funkcja jest stała.
b > 0 , bo wykres funkcji przecina oś OY powyżej osi OX, w punkcie (0,2).
Przykład 4
Określ znaki współczynników a i b funkcji korzystając z wykresu.
a < 0, bo funkcja jest malejąca.
b < 0 , bo wykres funkcji przecina oś OY poniżej osi OX, w punkcie
(0, – 1).
Przykład 5
Określ znaki współczynników a i b funkcji korzystając z wykresu.
a > 0, bo funkcja jest rosnąca.
b = 0 , bo wykres funkcji przechodzi przez początek układu współrzędnych, punkt (0, 0).
Przykład 6
Określ przez które ćwiartki układu współrzęnych przejdzie wykres funkcji, gdy a = 0 oraz b < 0.
Rozwiązanie
Rysujemy układ współrzędnych, numerujemy ćwiartki.
Rysujemy dowolny wykres funkcji spełniający dane z zadania.
a = 0, więc funkcja jest stała.
b < 0, więc funkcja musi przecinać oś OY poniżej osi OX, u nas w punkcie (0, – 2).
Wykres tej funkcji przechodzi przez I i II ćwiartkę.
Przykład 7
Określ przez które ćwiartki układu współrzęnych przejdzie wykres funkcji, gdy a > 0 oraz b > 0.
Rozwiązanie
Rysujemy układ współrzędnych, numerujemy ćwiartki.
Rysujemy dowolny wykres funkcji spełniający dane z zadania.
a > 0, więc funkcja jest rosnąca.
b > 0, więc funkcja musi przecinać oś OY powyżej osi OX, u nas w punkcie (0, 3).
Wykres funkcji przechodzi przez I, II oraz III ćwiartkę.
Przykład 8
Określ przez które ćwiartki układu współrzęnych przejdzie wykres funkcji, gdy a < 0 oraz b = 0.
Rozwiązanie
Rysujemy układ współrzędnych, numerujemy ćwiartki.
Rysujemy dowolny wykres funkcji spełniający dane z zadania.
a < 0, więc funkcja jest malejąca.
b = 0, więc funkcja musi przechodzić przez początek układu współrzędnych.
Wykres funkcji przechodzi przez II i IV ćwiartkę układu współrzędnych.